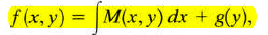Rafael Davis 4:07 am on June 7, 2017
Tags: math 15

Cauchy–Euler equation & power series

Cauchy–Euler equation

$x^{2}{\frac {d^{2}y}{dx^{2}}}+ax{\frac {dy}{dx}}+by=0.\,$

Case #1: Two distinct roots, m₁ and m₂
Case #2: One real repeated root, m
Case #3: Complex roots, α ± βi

In case #1, the solution is given by:

y=c_{1}x^{{m_{{1}}}}+c_{2}x^{{m_{2}}}\,

In case #2, the solution is given by

y=c_{1}x^{m}\ln(x)+c_{2}x^{m}\,

To get to this solution, the method of reduction of order must be applied after having found one solution y = x^m.

In case #3, the solution is given by:

y=c_{1}x^{\alpha }\cos(\beta \ln(x))+c_{2}x^{\alpha }\sin(\beta \ln(x))\,

\alpha ={\mathop {{\rm {Re}}}}(m)\,

\beta ={\mathop {{\rm {Im}}}}(m)\,

For

c_{1},c_{2}

∈ ℝ .

List of Maclaurin series of some common functions[edit]

\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}\,(x-a)^{n}

e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots

{\begin{aligned}{\frac {1}{1-x}}&=\sum _{n=0}^{\infty }x^{n}\\{\frac {1}{(1-x)^{2}}}&=\sum _{n=1}^{\infty }nx^{n-1}\\{\frac {1}{(1-x)^{3}}}&=\sum _{n=2}^{\infty }{\frac {(n-1)n}{2}}x^{n-2}.\end{aligned}}

${\begin{aligned}\sin x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}&&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots &&{\text{for all }}x\\[6pt]\cos x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}&&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots &&{\text{for all }}x\\[6pt]\tan x&=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}\left(1-4^{n}\right)}{(2n)!}}x^{2n-1}&&=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\cdots &&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\sec x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}}{(2n)!}}x^{2n}&&&&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\arcsin x&=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&&&{\text{for }}|x|\leq 1\\[6pt]\arccos x&={\frac {\pi }{2}}-\arcsin x\\&={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&&&{\text{for }}|x|\leq 1\\[6pt]\arctan x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&&&{\text{for }}|x|\leq 1,\ x\neq \pm i\end{aligned}}$

Ratio test

The usual form of the test makes use of the limit

L=\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|.

$L=\lim _{{n\to \infty }}\left|{\frac {a_{{n+1}}}{a_{n}}}\right|.$

L=\lim _{{n\to \infty }}\left|{\frac {a_{{n+1}}}{a_{n}}}\right|.

(1)

The ratio test states that:

if L < 1 then the series converges absolutely;
if L > 1 then the series is divergent;
if L = 1 or the limit fails to exist, then the test is inconclusive, because there exist both convergent and divergent series that satisfy this case.

Root test

\lim_{n\rightarrow\infty}\sqrt[n]{|a_n|},

converges then it equals C and may be used in the root test instead.

The root test states that:

if C < 1 then the series converges absolutely,
if C > 1 then the series diverges,
if C = 1 and the limit approaches strictly from above then the series diverges,
otherwise the test is inconclusive (the series may diverge, converge absolutely or converge conditionally).

There are some series for which C = 1 and the series converges, e.g.

\textstyle \sum 1/{n^{2}}

$\textstyle \sum 1/{n^2}$ , and there are others for which C = 1 and the series diverges, e.g. $\textstyle \sum 1/n$

$\textstyle\sum 1/n$ .

Integral test for convergence

Consider an integer

N

and a non-negative, continuous function

f

defined on the unbounded interval

[N, \infty)

, on which it is monotone decreasing. Then the infinite series

\sum _{n=N}^{\infty }f(n)

$\sum _{{n=N}}^{\infty }f(n)$

converges to a real number if and only if the improper integral

\int _{N}^{\infty }f(x)\,dx

$\int _{N}^{\infty }f(x)\,dx$

is finite. In other words, if the integral diverges, then the series diverges as well.

Alternating series test

A series of the form

\sum _{n=0}^{\infty }(-1)^{n}a_{n}=a_{0}-a_{1}+a_{2}-a_{3}+\cdots \!

$\sum _{n=0}^{\infty }(-1)^{n}a_{n}=a_{0}-a_{1}+a_{2}-a_{3}+\cdots \!$

where either all a_n are positive or all a_n are negative, is called an alternating series.

The alternating series test then says: if

a_{n}

$a_{n}$ decreases monotonically and $\lim _{n\to \infty }a_{n}=0$

$\lim _{{n\to \infty }}a_{n}=0$ then the alternating series converges.

Rafael Davis 10:18 pm on June 1, 2017
Tags: math 15

Laplace Transform and Gamma function

http://www.scienceforums.net/topic/8829-laplace-transform-and-gamma-function/

Screenshot from 2017-06-01 15-17-40

Rafael Davis 7:16 am on May 29, 2017
Tags: math 15

Variation of Parameters

(1)

(2)

y₁(t) and y₂(t) are a fundamental set of solutions.

find a pair of functions, u₁(t) and u₂(t) so that

Here’s the assumption. assume that whatever u₁(t) and u₂(t) are they will satisfy the following.

(3)

(4)

(5)

(6)

(7)

(8)

(9)

y^{(n)}(x) + \sum_{i=0}^{n-1} a_i(x) y^{(i)}(x) = b(x).\quad\quad {\rm (i)}

Let

y_1(x), \ldots, y_n(x)

be a fundamental system of solutions of the corresponding homogeneous equation

y^{(n)}(x) + \sum_{i=0}^{n-1} a_i(x) y^{(i)}(x) = 0.\quad\quad {\rm (ii)}

Then a particular solution to the non-homogeneous equation is given by

y_p(x) = \sum_{i=1}^{n} c_i(x) y_i(x)\quad\quad {\rm (iii)}

The particular solution to the non-homogeneous equation can then be written as

\sum_{i=1}^n y_i(x) \, \int \frac{W_i(x)}{W(x)}\ \mathrm dx.

Rafael Davis 4:32 am on May 29, 2017
Tags: math 15

Math 15 note Laplace transform

ANNIHILATOR APPROACH

Given $y''-4y'+5y=\sin(kx)$ , $P(D)=D^{2}-4D+5$ . The simplest annihilator of $\sin(kx)$ is $A(D)=D^{2}+k^{2}$ . The zeros of $A(z)P(z)$ are $\{2+i,2-i,ik,-ik\}$ , so the solution basis of $A(D)P(D)$ is $\{y_{1},y_{2},y_{3},y_{4}\}=\{e^{{(2+i)x}},e^{{(2-i)x}},e^{{ikx}},e^{{-ikx}}\}.$

Setting

y=c_{1}y_{1}+c_{2}y_{2}+c_{3}y_{3}+c_{4}y_{4}

we find

{\begin{aligned}\sin(kx)&=P(D)y\\[8pt]&=P(D)(c_{1}y_{1}+c_{2}y_{2}+c_{3}y_{3}+c_{4}y_{4})\\[8pt]&=c_{1}P(D)y_{1}+c_{2}P(D)y_{2}+c_{3}P(D)y_{3}+c_{4}P(D)y_{4}\\[8pt]&=0+0+c_{3}(-k^{2}-4ik+5)y_{3}+c_{4}(-k^{2}+4ik+5)y_{4}\\[8pt]&=c_{3}(-k^{2}-4ik+5)(\cos(kx)+i\sin(kx))+c_{4}(-k^{2}+4ik+5)(\cos(kx)-i\sin(kx))\end{aligned}}

giving the system

i=(k^{2}+4ik-5)c_{3}+(-k^{2}+4ik+5)c_{4}

0=(k^{2}+4ik-5)c_{3}+(k^{2}-4ik-5)c_{4}

which has solutions

c_{3}={\frac i{2(k^{2}+4ik-5)}}

c_{4}={\frac i{2(-k^{2}+4ik+5)}}

giving the solution set

{\begin{aligned}y&=c_{1}y_{1}+c_{2}y_{2}+{\frac i{2(k^{2}+4ik-5)}}y_{3}+{\frac i{2(-k^{2}+4ik+5)}}y_{4}\\[8pt]&=c_{1}y_{1}+c_{2}y_{2}+{\frac {4k\cos(kx)-(k^{2}-5)\sin(kx)}{(k^{2}+4ik-5)(k^{2}-4ik-5)}}\\[8pt]&=c_{1}y_{1}+c_{2}y_{2}+{\frac {4k\cos(kx)+(5-k^{2})\sin(kx)}{k^{4}+6k^{2}+25}}.\end{aligned}}

y_{p}={\frac {4k\cos(kx)+(5-k^{2})\sin(kx)}{k^{4}+6k^{2}+25}}

y_{c}=e^{2x}(c_{1}\cos x+c_{2}\sin x)

y_{c}=e^{{2x}}(c_{1}\cos x+c_{2}\sin x)

Laplace Transform

Sufficient Conditions for Existence
f(t) is piecewise continuous on the interval [O, oo) and of exponetial order

F(s) ->0 as s -> oo

		conditions
1

Properties of the unilateral Laplace transform
	Time domain	$s$ domain	Comment
Linearity	$af(t)+bg(t)\$	$aF(s)+bG(s)\$	Can be proved using basic rules of integration.
Frequency-domain derivative	$tf(t)\$	$-F'(s)\$	$F'$ is the first derivative of $F$ with respect to $s$ .
Frequency-domain general derivative	$t^{n}f(t)\$	$(-1)^{n}F^{(n)}(s)\$	More general form, $n$ th derivative of $F (s)$ .
Derivative	$f'(t)\$	$sF(s)-f(0)\$	$f$ is assumed to be a differentiable function, and its derivative is assumed to be of exponential type. This can then be obtained by integration by parts
Second derivative	$f''(t)\$	$s^{2}F(s)-sf(0)-f'(0)\$	$f$ is assumed twice differentiable and the second derivative to be of exponential type. Follows by applying the Differentiation property to $f'(t)$ .
General derivative	$f^{(n)}(t)\$	$s^{n}F(s)-\sum _{k=1}^{n}s^{n-k}f^{(k-1)}(0)\$	$f$ is assumed to be $n$ -times differentiable, with $n$ th derivative of exponential type. Follows by mathematical induction.
Frequency-domain integration	${\frac {1}{t}}f(t)\$	$\int _{s}^{\infty }F(\sigma )\,d\sigma \$	This is deduced using the nature of frequency differentiation and conditional convergence.
Time-domain integration	$\int _{0}^{t}f(\tau )\,d\tau =(u*f)(t)$	${1 \over s}F(s)$	$u (t)$ is the Heaviside step function and $(u * f)(t)$ is the convolution of $u (t)$ and $f (t)$ .
Frequency shifting	$e^{at}f(t)\$	$F(s-a)\$
Time shifting	$f(t-a)u(t-a)\$	$e^{-as}F(s)\$	$u (t)$ is the Heaviside step function
Time scaling	$f(at)$	${\frac {1}{a}}F\left({s \over a}\right)$	$a>0\$
Multiplication	$f(t)g(t)$	${\frac {1}{2\pi i}}\lim _{T\to \infty }\int _{c-iT}^{c+iT}F(\sigma )G(s-\sigma )\,d\sigma \$	The integration is done along the vertical line Re(σ) = c that lies entirely within the region of convergence of $F$ .^[15]
Convolution	$(f*g)(t)=\int _{0}^{t}f(\tau )g(t-\tau )\,d\tau$	$F(s)\cdot G(s)\$
Complex conjugation	$f^{*}(t)$	$F^{}(s^{})$
Cross-correlation	$f(t)\star g(t)$	$F^{}(-s^{})\cdot G(s)$
Periodic function	$f(t)$	${1 \over 1-e^{-Ts}}\int _{0}^{T}e^{-st}f(t)\,dt$	$f (t)$ is a periodic function of period $T$ so that $f (t) = f (t + T)$ , for all $t \geq 0$ . This is the result of the time shifting property and the geometric series.

f(0^{+})=\lim _{s\to \infty }{sF(s)}.

https://www.youtube.com/watch?v=OiNh2DswFt4&list=PL96AE8D9C68FEB902&index=26

Rafael Davis 12:48 am on May 29, 2017
Tags: math 15

Math 15 notes

existence of a unique solution

Consider the following IVP.

If f(t,y) and

are continuous functions in some rectangle

containing the point (t_o, y_o) then there is a unique solution to the IVP in some interval t_o

h < t < t_o + h that is contained in

First order homogeneous equation:

A first-order ordinary differential equation in the form:

M(x,y)\,dx+N(x,y)\,dy=0

M(x,y)\,dx+N(x,y)\,dy=0

is a homogeneous type if both functions M(x, y) and N(x, y) are homogeneous functions of the same degree n.^[1] That is, multiplying each variable by a parameter

\lambda

\lambda

, we find

M(\lambda x,\lambda y)=\lambda ^{n}M(x,y)\,

M(\lambda x, \lambda y) = \lambda^n M(x,y)\,

and

N(\lambda x,\lambda y)=\lambda ^{n}N(x,y)\,.

$N(\lambda x,\lambda y)=\lambda ^{n}N(x,y)\,.$

Solution method
Introduce the change of variables ${\displaystyle y=ux}$

$y=ux$ ;

Exact differential equation

Given a simply connected and open subset D of R² and two functions I and J which are continuous on D then an implicit first-order ordinary differential equation of the form

I(x,y)\,\mathrm {d} x+J(x,y)\,\mathrm {d} y=0,\,\!

I(x, y)\, \mathrm{d}x + J(x, y)\, \mathrm{d}y = 0, \,\!

is called an exact differential equation if there exists a continuously differentiable function F, called the potential function, so that

{\frac {\partial F}{\partial x}}=I

\frac{\partial F}{\partial x} = I

and

{\frac {\partial F}{\partial y}}=J.

\frac{\partial F}{\partial y} = J.

Solutions to exact differential equation

685adf38-067e-4336-a92e-9e39b8dca6bc (2).png

substitute g(y) into

685adf38-067e-4336-a92e-9e39b8dca6bc (1).png

linear Equation and integrating factor

Proof:

{\displaystyle y’+P(x)y=Q(x)}

y'+P(x)y=Q(x)

{\displaystyle M(x)}

M(x)

, integrating factor

M(x)=e^{\int _{s_{0}}^{x}P(s)ds}

M(x)=e^{{\int _{{s_{0}}}^{{x}}P(s)ds}}

then:

{\begin{aligned}(1)\qquad &M(x){\underset {\text{partial derivative}}{(\underbrace {y’+P(x)y} )}}\\(2)\qquad &M(x)y’+M(x)P(x)y\\(3)\qquad &{\underset {\text{total derivative}}{\underbrace {M(x)y’+M'(x)y} }}\end{aligned}}

{\begin{aligned}(1)\qquad &M(x){\underset {{\text{partial derivative}}}{(\underbrace {y'+P(x)y})}}\\(2)\qquad &M(x)y'+M(x)P(x)y\\(3)\qquad &{\underset {{\text{total derivative}}}{\underbrace {M(x)y'+M'(x)y}}}\end{aligned}}

Going from step 2 to step 3 requires that

{\displaystyle M(x)P(x)=M'(x)}

M(x)P(x)=M'(x)

{\displaystyle {\begin{aligned}(4)\qquad &M(x)P(x)=M'(x)\\(5)\qquad &P(x)={\frac {M'(x)}{M(x)}}\\(6)\qquad &\int _{s_{0}}^{x}P(s)ds=\ln M(x)\\(7)\qquad &e^{\int _{s_{0}}^{x}P(s)ds}=M(x)\end{aligned}}}

${\begin{aligned}(4)\qquad &M(x)P(x)=M'(x)\\(5)\qquad &P(x)={\frac {M'(x)}{M(x)}}\\(6)\qquad &\int _{s_{0}}^{x}P(s)ds=\ln M(x)\\(7)\qquad &e^{\int _{s_{0}}^{x}P(s)ds}=M(x)\end{aligned}}$